Source: Time
If a, b and c are three-digit positive integers satisfying a + b = c, is the units digit of c the sum of the units digits of a and b?
(1) The hundreds digit of c is equal to the sum of the hundreds digits of a and b. The units digit of c is at least equal to the sum of the units digits of a and b.
(2) The sum of the digits of c is not more than the sum of the digits of a and b.
If a, b and c are three-digit positive integers
This topic has expert replies
- conquistador
- Master | Next Rank: 500 Posts
- Posts: 266
- Joined: Fri Sep 19, 2014 4:00 am
- Thanked: 4 times
- Followed by:1 members
GMAT/MBA Expert
- ceilidh.erickson
- GMAT Instructor
- Posts: 2095
- Joined: Tue Dec 04, 2012 3:22 pm
- Thanked: 1443 times
- Followed by:247 members
The structure of this question is very strange. The first statement actually contains two statements within it - they could be evaluated separately. The GMAT won't actually do this.
But, let's break down this question...
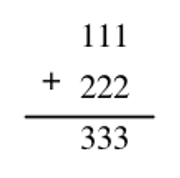
If the sum of the units digits in a and b is greater than 10, the excess will spill over into the tens digit place:
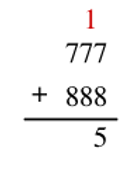
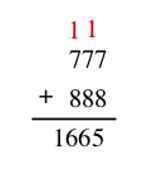
So really, our target question is: Is the sum of the units digits of a and b less than 10?
Now for the weird statements:
But, let's break down this question...
When we add multi-digits numbers together, the units digit of the resulting sum will be the same as the sum of the units digits only if the units digits add up to less than 10. Consider:If a, b and c are three-digit positive integers satisfying a + b = c, is the units digit of c the sum of the units digits of a and b?
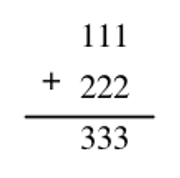
If the sum of the units digits in a and b is greater than 10, the excess will spill over into the tens digit place:
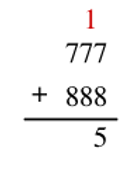
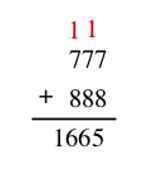
So really, our target question is: Is the sum of the units digits of a and b less than 10?
Now for the weird statements:
(1) The hundreds digit of c is equal to the sum of the hundreds digits of a and b. The units digit of c is at least equal to the sum of the units digits of a and b. [ /quote]
If we just took the first part - The hundreds digit of c is equal to the sum of the hundreds digits of a and b - that would tell us that there's no spillover into the hundreds digit. That tells us that the sum of the tens digits must have been less than 10. But that doesn't answer our target question about units digits, so insufficient.
But now let's add on the unrelated second piece - The units digit of c is at least equal to the sum of the units digits of a and b. So consider our two examples above. When the sum of the units digits of a and b was less than 10, the units digit of c was exactly equal to the sum (1 + 2 = 3). When the sum of the units digits of a and b was greater than 10, though, the units digit of c was less than that sum (7 + 8 = 5??). If the units digit of c is less than the sum of the units digits of a and b, that means there was spillover! We can never get a units digit that greater than the sum
So, this piece of statement 1 was sufficient on its own. (Which really means that it should have been its own statement!)
For this one, let's test the examples that we have above. In the first example:(2) The sum of the digits of c is not more than the sum of the digits of a and b.
3 + 3 + 3 = 9
1 + 1 + 1 + 2 + 2 + 2 = 9
If we have no spillover, the digits of c will add up exactly to the sum of the digits of a and b.
In the second example:
1 + 6 + 6 + 5 = 18
7 + 7 + 7 + 8 + 8 + 8 = 45
If there is spillover, the sum of the digits of c will always be less than the sum of the digits of a and b.
But this statement says "The sum of the digits of c is not more than the sum of the digits of a and b." But it will NEVER be more! So this statement really tells us nothing at all!
Technically, the answer here is A. But it's such a poorly structured question that that's almost irrelevant. I would avoid studying from this source.
Ceilidh Erickson
EdM in Mind, Brain, and Education
Harvard Graduate School of Education
EdM in Mind, Brain, and Education
Harvard Graduate School of Education
-
Matt@VeritasPrep
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
Given a three digit integer xyz, we know that its sum can be represented as 100x + 10y + z. (For instance, 543 = 5*100 + 4*10 + 3.)
Let's say that a = rst, b = uvw, and c = xyz. We're told that
100r + 10s + t + 100u + 10v + w = 100x + 10y + z, or
100(r + u) + 10(s + v) + (w + t) = 100x + 10y + z
We want to know if z = (w + t).
S1:: x = (r + u) AND z ≥ (w + t).
Going back to our equation, since (r + u) = x, we can subtract 100(r + u) and 100x from both sides, since they are equal. This leaves us with
10(s + v) + (w + t) = 10y + z, which can be reduced to
10(s + v - y) = z - (w + t)
Notice that the RHS consists of three single digit integers, so its sum is anywhere from 9 (when z = 9 and w+t = 0) to -18 (when z = 0 and w+t = 18). Also notice that z - (w + t) is EQUAL to a multiple of 10, since it equals 10 * (s + v - y). Thus the only multiples of 10 possible are 0 and -10.
If z - (w + t) = 0, then z = (w + t), and we're set.
If z - (w + t) = -10, then z = (w + t) - 10. But then (w + t) > z, contradicting the info we were just given (i.e. that z ≥ (w + t)).
Hence z - (w + t) = 0, and S1 is sufficient.
S2::
x + y + z ≤ r + s + t + u + v + w
Not very helpful, since we can't isolate z, w, and t.
Let's say that a = rst, b = uvw, and c = xyz. We're told that
100r + 10s + t + 100u + 10v + w = 100x + 10y + z, or
100(r + u) + 10(s + v) + (w + t) = 100x + 10y + z
We want to know if z = (w + t).
S1:: x = (r + u) AND z ≥ (w + t).
Going back to our equation, since (r + u) = x, we can subtract 100(r + u) and 100x from both sides, since they are equal. This leaves us with
10(s + v) + (w + t) = 10y + z, which can be reduced to
10(s + v - y) = z - (w + t)
Notice that the RHS consists of three single digit integers, so its sum is anywhere from 9 (when z = 9 and w+t = 0) to -18 (when z = 0 and w+t = 18). Also notice that z - (w + t) is EQUAL to a multiple of 10, since it equals 10 * (s + v - y). Thus the only multiples of 10 possible are 0 and -10.
If z - (w + t) = 0, then z = (w + t), and we're set.
If z - (w + t) = -10, then z = (w + t) - 10. But then (w + t) > z, contradicting the info we were just given (i.e. that z ≥ (w + t)).
Hence z - (w + t) = 0, and S1 is sufficient.
S2::
x + y + z ≤ r + s + t + u + v + w
Not very helpful, since we can't isolate z, w, and t.


















